Measurement of Voltage Using CRO
Cathode Ray Oscilloscope (CRO) is primary a voltage-measuring instrument. Once we have measured the voltage, other quantities can be calculated. CRO is a voltage dependent instrument and can be used for the measurement of voltages at any frequency within the range of the operation of the CRO.
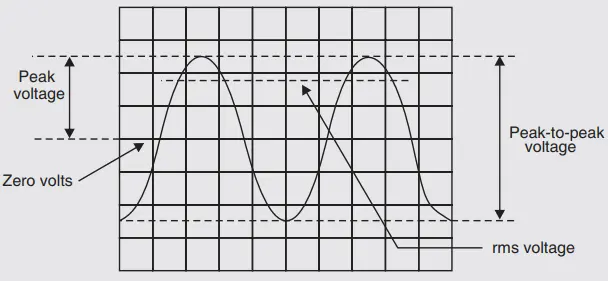
Fig. 1. shows the display of voltage. To measure the voltages
- The input voltage is applied on the vertical deflection plates.
- An appropriate sweep is applied to the horizontal plates.
- The amplitude attenuator is than adjusted such that the signal is displayed comfortably on the screen.
- The amplitude trace of the waveform is then observed on the screen.
- The position of the attenuator knob gives the volts/cm position or volts/ division.
- The peak to peak voltage of the input signal is measured by multiplying this position value with the number of centimeters the signal is occupying in the vertical direction.
- The peak to peak voltage of the signal is given by
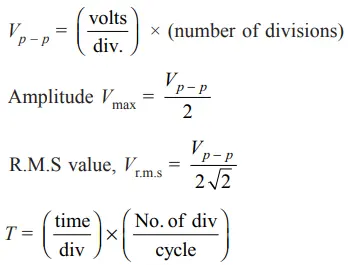
EXAMPLE: The waveform shown in Fig. 2 is observed on the screen of an oscilloscope. If the vertical attenuation is set to 0.5 V/div, determine the peak to peak amplitude of the signal.
SOLUTION: Given: Volts/div = 0.5 V and number of divisions along the vertical axis = 3,
We know that the peak to peak voltage,
Vp – p = (volts/div) × no. of div = 0.5 V × 3 = 1.5 Vp – p Ans.
EXAMPLE : Fig 3 shows the waveform of a sinusoidal voltage observed on CRO. The vertical attenuation selected is 2 mV/div. Calculate the amplitude and RMS value of the sinusoidal voltage.
SOLUTION: Given: Volts/Division = 2 mV/div
It can be observed that the one part is subdivided into 5 units.
1 subdivision = 1/5 = 0.2 units
It can also be observed that positive peak of signal corresponds to two full divisions and three subdivisions. Thus positive peak is,
Positive Peak = (2 full divisions) + (3 subdivisions × value of 1 subdivision) = 2 + 3 × 0.2 = 2.6 divisions
Similarly for negative peak,
Negative Peak = 2.6 divisions
Then peak-to-peak voltage Vp – p = 2.6 + 2.6 = 5.2 divisions
V p – p = Number of divisions × (volts /division) = 5.2 × 2 mV = 10.4 mV
We know that the amplitude of the waveform is given by,
Vp = Vp-p /2 = 10.4/2 = 5.2 mV Ans.
We also know that the RMS value of the waveform, VRMS = Vp/2 = 5.2/ √2 = 3.6769 mV Ans.
Measurement of Current
Current cannot be measured directly with a CRO. To measure the current, a known resistance is taken and the potential drop across the resistance is determined with the help of measurement of potential at both ends of the resistor. The voltage across resistance is displayed on CRO and measured. The voltage divided by the considered resistance value gives the amount of current flowing in the device.
Measurement of Time Period
The waveform is displayed on the screen such that one complete cycle is visible on the screen. Note the time/division on the front panel. Then the period of the waveform can be obtained as,
T = Time/Division × number of divisions occupied by one cycle
Frequency without Lissajous pattern, f = 1/T
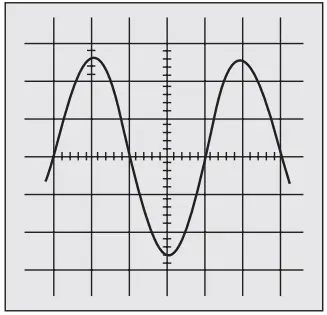
Example: If the time/div control is set to 2 µs/div when the waveform in Fig. 4, is displayed on the CRT screen, determine the frequency of the signal.
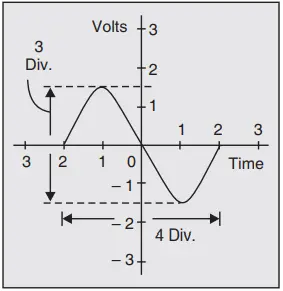
Solution: The period of the signal is calculated using the equation,
T = (time/div) x (No. of div/cycle) = 2 µs × 4 = 8 ms
Frequency is given by, f = 1/T = 1/8 µs = 125 kHz Ans.
Lissajous Figures
Lissajous Figures (or patterns) are named in honour of the French scientist who first obtained them geometrically and optically. They illustrate one of the earliest uses to which the CRO was put.
Lissajous patterns are formed when two sine waves are applied simultaneously to the vertical and horizontal deflecting plates of a CRO. The two sine waves may be obtained from two audio oscillators as shown in Fig. 5.
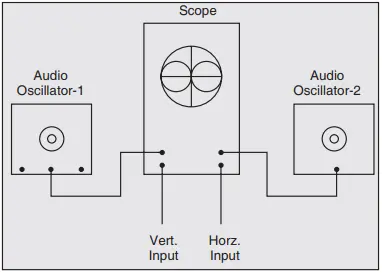
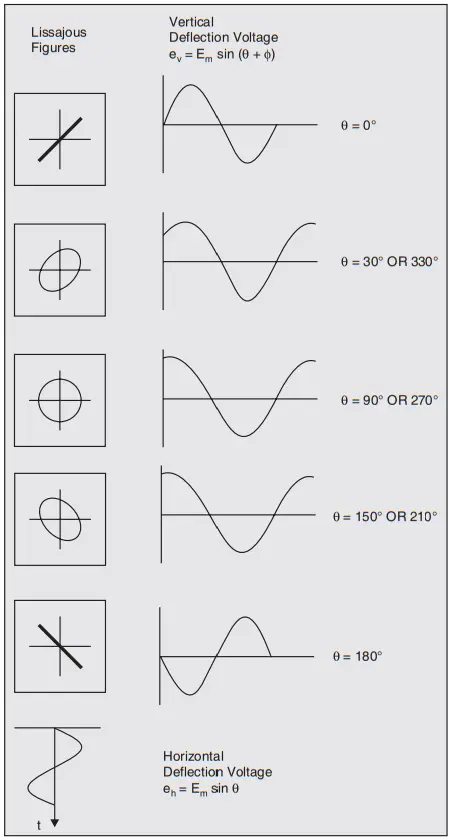
Obviously, in this case, a sine wave sweeps a sine-wave input signal. The shape of the Lissajous pattern depends on the frequency and phase relationship of the two sine waves. Two sine waves of the same frequency and amplitude may produce a straight line, an ellipse or a circle depending on their phase difference as shown in Fig. 6.
In general, the shape of Lissajous Figures depends on
- Amplitude
- Phase difference
- Ratio of frequency of the two waves.
Consider the two signals applied having same amplitude and frequency with phase difference of Ø between them,
eH = Em sin θ
eV = Em sin (θ + Ø)
Straight Line:
- The straight line is formed when the two voltages are in phase with each other or 180° out of phase with each other.
- The straight line formed angle 45° with horizontal when the magnitude of voltages are equal.
- An increase in vertical deflection voltage causes the line to have an angle greater than 45°with the horizontal.
- A grater horizontal voltage makes the angle less than 45 ° with the horizontal.
Circle: When the magnitudes of two voltages are equal and the phase difference between them is either 90° or 270°
Ellipse: The ellipse is formed when voltage are not equal and or out of phase.
Use of Lissajous Figures
Lissajous Figures are used as:
- determining an unknown frequency by comparing it with a known frequency
- checking audio oscillator with a known-frequency signal
- checking audio amplifiers and feedback networks for phase shift.
Frequency Determination with Lissajous Figures
The unknown signal is applied across one set of deflecting plates and a known signal across the other. By studying the resultant Lissajous pattern, unknown frequency can be found. Depending on the frequency ratio, the various patterns obtained are shown in Fig. 7.
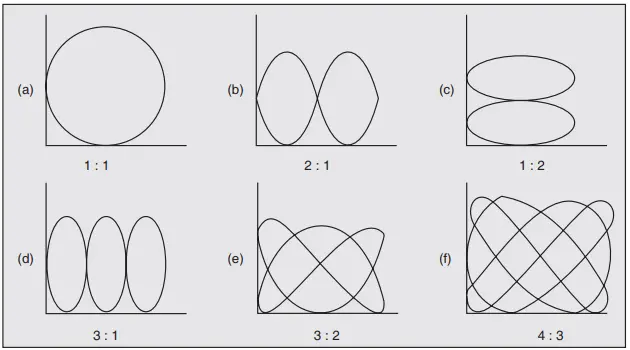
The ratio of the two frequencies is given by
fV/f H = No. of points of horizontal tangency ÷ No. of points of vertical tangency
In Fig. 7 (a), there is one point of tangency along the horizontal as well as vertical axis. Hence, fH = fV i.e. the signals have the same frequency.
The ratio of frequencies when open ended Lissajous patterns are obtained can also be found by treating the open ends as half tangencies as shown in Fig. 8.
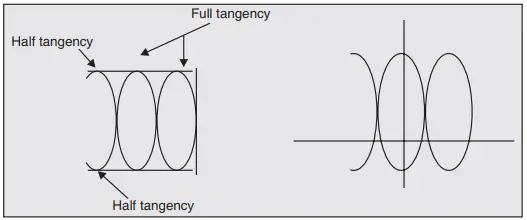
fV /fH = (No. of points of horizontal tangency + ½) ÷ No. of points of vertical tangency
For Fig. 8 we get, fV /fH = (2 + ½) ÷ 1 = 5/2
It should be noted that this method of frequency determination has limitations and is being discarded gradually because low-cost digital frequency counters are available in the market. The two main limitations of this method are as under:
- the numerator and denominator of the frequency ratio must be whole numbers,
- the maximum ratio of frequencies that can be used is 10 : 1. Beyond that, the Lissajous patterns become too complex to analyze.
EXAMPLE: A Lissajous pattern on the oscilloscope is stationary having 8 vertical maximum values and 6 horizontal maximum values. Calculate the frequency of vertical input if the frequency of horizontal input is 1800 Hz.
SOLUTION: Given: fH = 1800 kHz, number of vertical tangencies = 8 and number of horizontal tangencies = 6
We know that, fH/fV = Number of horizontal tangencies ÷ Number of vertical tangencies
fV/1800 = 6/8
fV = 2400 Hz Ans.
Phase Determination with Lissajous Figures
A Lissajous pattern is obtained on CRO with an unknown phase difference Ø. This pattern which is in the form of an ellipse, provides a simple means of finding phase difference between two voltages.
The gains of the vertical amplifiers are adjusted so that the ellipse fits exactly into a square marked by the lines on the graticule.
If the major axis lies in first and third quadrants: If the major axis of the ellipse lies on the first and third quadrants, its slope is positive as shown is Fig. 9.
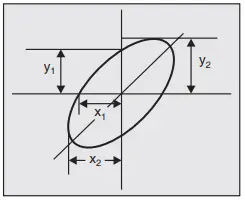
Then the phase angle is either between 0° and 90° or between 270° and 360°. The sine of the phase angle between the voltages is given by
sin Ø = Y1/Y2 = X1 /X 2
Ø = sin-1(Y1/Y2)
If the major axis in lies in second and forth quadrants: If the major axis of the ellipse lies on the second and forth quadrants, its slope is negative as shown in Fig. 10.
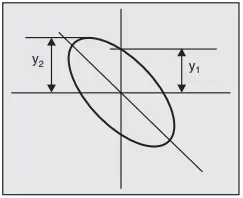
Then the phase angle is either between 90° and 180° or between 180° and 270°. The sin of the phase angle between the voltages is given by
Ø = 180o – sin-1(Y1/Y2)
EXAMPLE: The Lissajous Figure obtained on the CRO is shown in Fig. 11. Find the phase difference between the two waves applied.
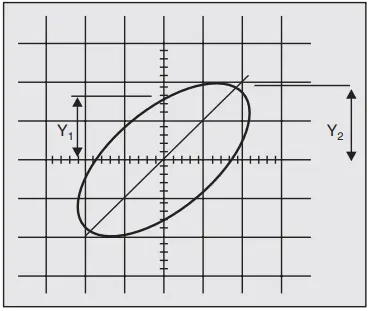
SOLUTION: From the Lissajous Figure shown in Fig 7.35, we know that Y1 = 8 units; Y2 = 10 units
We know that if the major axis lies in first and third quadrants then phase difference is given by, Ø = sin-1(Y1/Y2)
= sin–1 (8/10) = 53.13° Ans.